Compactness is Preserved Under Continuous Functions

One key topology homeomorphism invariant is compactness, a fact fundamental to the extreme value theorem.

Proof

The main strategy here is to take an arbitrary open cover of $f(X^{\prime })$, use continuity with images to induce an open cover of $X$, which has a finite subcover, which can then be used to find a corresponding finite subcover of $f(X^{\prime })$ in the codomain.

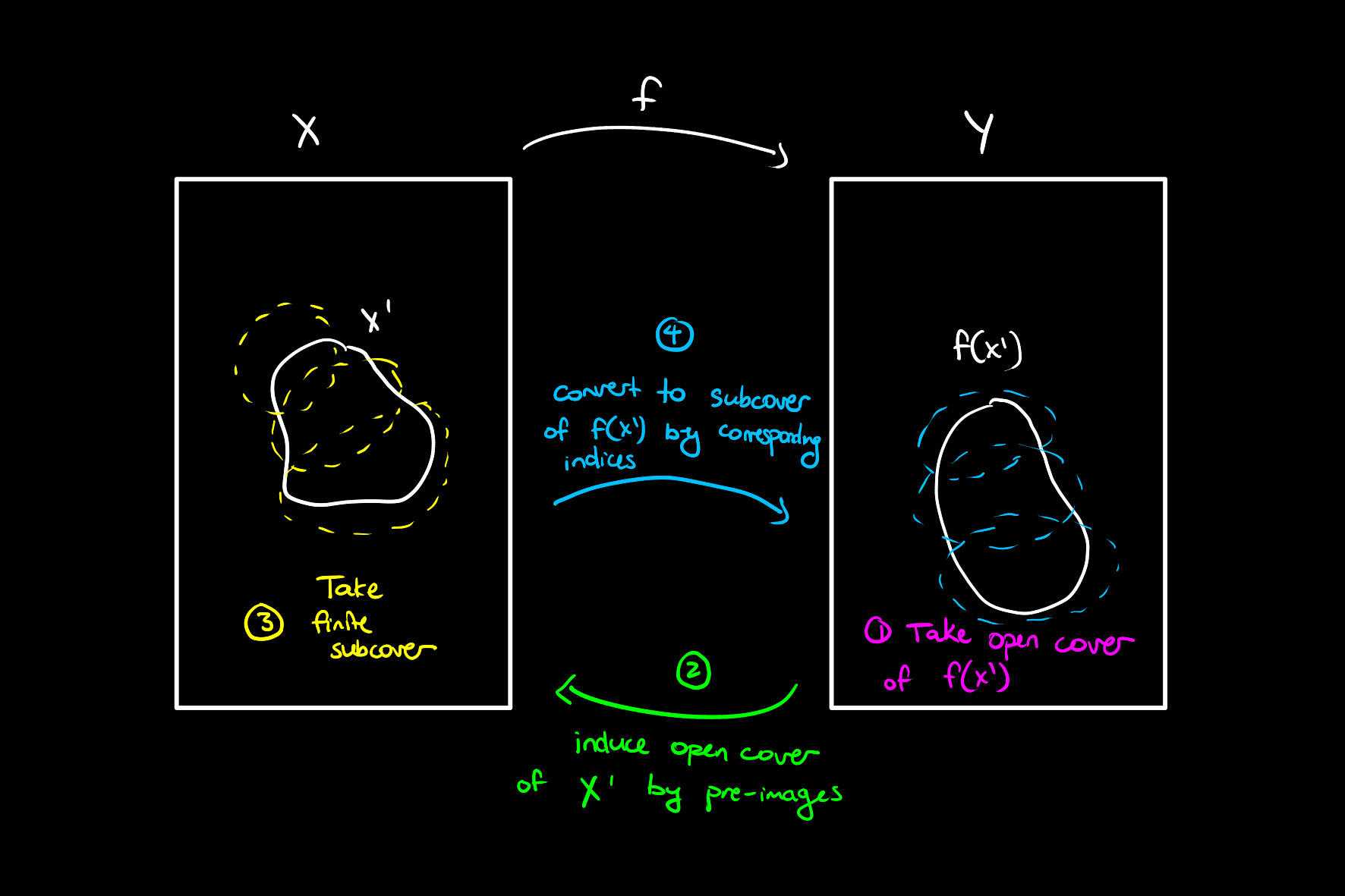
Consider an arbitrary open cover of $f(X^{\prime })$, that is

Then, since pre-images preserve unions,

First we show that this set is an open cover of $X^{\prime }$.

Each set is open from continuity of $f$ and openness of $V_i$ for each $i$.

Then because pre-images preserve inclusions and any set is a subset of the pre-image of its image under some function, we have that

and hence the desired set covers $X^{\prime }$, this cover has a finite subcover, namely a finite subset $J\subseteq I$ such that

is an open cover of $X^{\prime }$.

We will now prove that the corresponding indices give a subcover of $f(X^{\prime })$, that is that

is a finite cover of $f(X^{\prime })$ which is a subcover of our original cover.

Clearly this cover is open, and finite, we simply must prove that it does indeed cover $f(X^{\prime })$.

Now, for each $y\in f(X^{\prime })$, there exists and $x\in X^{\prime }$ such that $f(x)=y$. Then, since $\bigcup _{j\in J}{f}^{-1}(V_j)$ covers $X^{\prime }$, we know that $x\in V_j$ for some $j\in J$ and hence $f(x)=y\in f(V_j)$ for the same $j$. This means for any $y\in f(X^{\prime })$, our finite subcover contains $y$, and thus it covers $f(X^{\prime })$.